Quality of Search Engine - PageRank

Web search engines such as Google.com distinguish themselves by the qualtiy of their returns to search queries. I will discuss a rough approximation of Google’s method for judging the qualtiy of web pages by using PageRank.

Introduction

When a web search is initiated, there is rather a complex series of tasks that are carried out by the search engine. One obvious task is word-matching, to find pages that contain the query words, in the title or body of the page. Another key task is to rate the pages that are identified by the first task, to help the user wade through the possibly large set of choices. This is basically how information retrieval task works!

PageRank

When you google for a keyword “steak sauce”, it would possibly return several million pages, begining with the some recipes for steak, a reasonably outcome. How is this ranking determined? The answer to this question is that Google.com assigns a non-negative real number, called the page rank, to each web page that it indexes.

Consider a graph like the following:

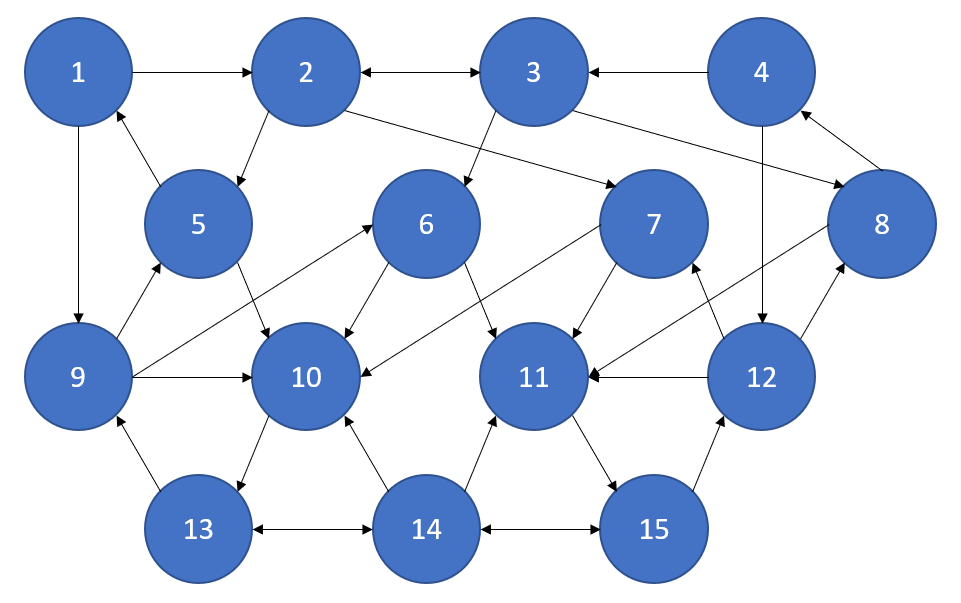
Each of $n$ nodes represents a web page, and a directed edge from node to means that page contains a web link to page . Let denote the adjacency matrix, an matrix whose -th entry is 1 if there is a link from node to node , and 0 otherwise.

The invention of Google imagined a surfer on a network of pages, who currently sits at page with probability . Next, the surfer either moves to a random page (with fixed probability , often around 0.15) or with probability , clicks randomly on a link from the current page . The probability that the surfer moves from page to page after the click is

where is the entry of the adjacency matrix , and is the sum of the -th row of . Since the time is arbitrary, the probability of being at node is the sum of this expression over all , and it is independent of time; that is,

which is equivalent in matrix terms to the eigenvalue equation

where

Let’s contruct the adjacency matrix using MATLAB!

%% Construct adjacency matrix A, there are 34 arrows
clear all; clc
n = 15
i = [5 1 3 2 4 8 2 9 3 9 2 12 3 12 1 13 5 6 7 9 14 6 7 8 12 14 4 15 10 14 13 15 11 14];
j = [1 2 2 3 3 4 5 5 6 6 7 7 8 8 9 9 10 10 10 10 10 11 11 11 11 11 12 12 13 13 14 14 15 15];
A = sparse(i, j, 1, n, n);
full(A);

We also know that , , and are non-negative, so . Since the total of transition probability from a state to all other states must be1, that is, by the construction of the sum of all non-negative elements inside each matrix column is equal to unity, thus this Google matrix $G$ is a stochastic matrix.

In mathematics, a stocastic matrix is a square matrix used to describe the transitions of a Markov chain. Each of the entries is a non-negative real number representing a probability. It is also called a probability matrix, transition matrix, or Markov matrix.

Next step is to contruct the matrix for the network, and verify the given dominant eigenvector .

%% Construct google matrix G
G = zeros(n, n)
q = 0.15
for i = 1:n
    for j = 1:n
        G(i, j) = q/n + A(j, i) * (1-q) / sum(A(j, :));
    end
end

We also define a power method to computeeigen values and eigenvectors.

function [V, D] = power(A, iter)
    % Power Method
    [m, n] = size(A);
    % Random number generator
    rng(1)
    % Initial vector
    x0 = randn(n, 1);
    x = x0;
    for j = 1:iter
        u = x / norm(x);
        x = A * u;
        % Rayleigh Quotient
        lam = u' * x;
        L(j) = lam;
    end
    % Eigenvalue D
    D = L(end);
    u = x / norm(x);
    % Eigenvector V
    V = u;

We use the above function to find the dominant eigenvector .

iter = 1000;
[p, D] = power(G, iter);
p = p / sum(p);

The entries of represents the importance level of each 15 websites.

%---------- Results ----------%
p = 
    0.0268
    0.0299
    0.0299
    0.0268
    0.0396
    0.0396
    0.0396
    0.0396
    0.0746
    0.1063
    0.1063
    0.0746
    0.1251
    0.1163
    0.1251

Jump Probability

What is the purpose of the jump probability? There is some probability such that at every step the walk has an probability of jumping to a uniformly chosen random page. They tell us that is set to some moderately small constant like 0.15. This is equivalent to adding a low-weight edge between every pair of vertices.

You may wonder what if we change the jump probability ? I describe the resulting changes below.

page	q = 0.15	q = 0	q = 0.5
1	0.0268	0.0154	0.0467
2	0.0299	0.0116	0.0540
3	0.0299	0.0116	0.0540
4	0.0268	0.0154	0.0467
5	0.0396	0.0309	0.0536
6	0.0396	0.0309	0.0536
7	0.0396	0.0309	0.0536
8	0.0396	0.0309	0.0536
9	0.0746	0.0811	0.0676
10	0.1063	0.1100	0.0946
11	0.1063	0.1100	0.0946
12	0.0746	0.0811	0.0676
13	0.1251	0.1467	0.0905
14	0.1163	0.1467	0.0786
15	0.1163	0.1467	0.0905

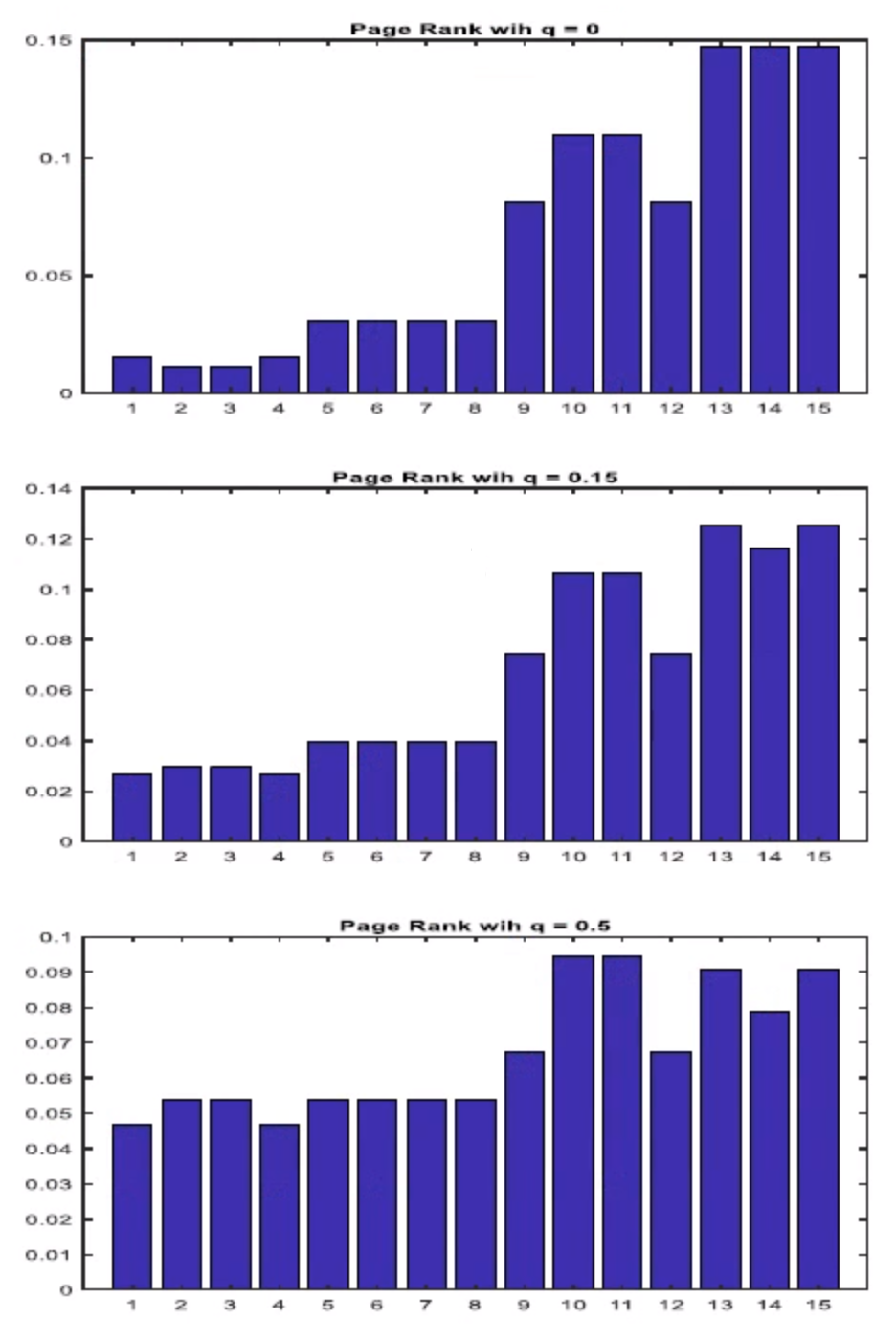
How does PageRank work for disjoint connected components? PageRank “fixes” this with the “teleportation” parameter, famously set to 0.15, that weakly connects all nodes to all other nodes. This can be thought of as an implicit link to all other nodes in the graph with weight . Making this teleportation factor higher should allow a higher probability of escaping from a small connected component.

Without transportation, PageRank doesn’t provide a way to compute the centralities of nodes in different components. That is, computing the PageRank of a node tells you its relative importance “within that component”, but doen’t tell anything about how different components compare.

Suppose that Page 7 in the network wanted to improve its page rank, compared with its competitor Page 6, by persuading Pages 2 and 12 to more prominently display its links to Page 7. Model this by replacing and by 2 in the adjacency matrix. Let’s see whether this strategy succeed or not.

%% Construct adjacency matrix A
n = 15
i = [5 1 3 2 4 8 2 9 3 9 2 12 3 12 1 13 5 6 7 9 14 6 7 8 12 14 4 15 10 14 13 15 11 14];
j = [1 2 2 3 3 4 5 5 6 6 7 7 8 8 9 9 10 10 10 10 10 11 11 11 11 11 12 12 13 13 14 14 15 15];
A = sparse(i, j, 1, n, n);
A(2, 7) = 2;
A(12, 7) = 2;
full(A);

%% Construct Google Matrix
G = zeros(0)
q = 0.15
for i = 1:n
    for j = 1:n
        G(i, j) = q/n + A(j, i) * (1-q) / sum(A(j, :));
    end
end

%% Solve eigenvalue problem for the ranking vector
iter = 1000;
[p, D] = power(G, iter);
p = p / sum(p);
bar(p);
title('PageRank with q = 0.15');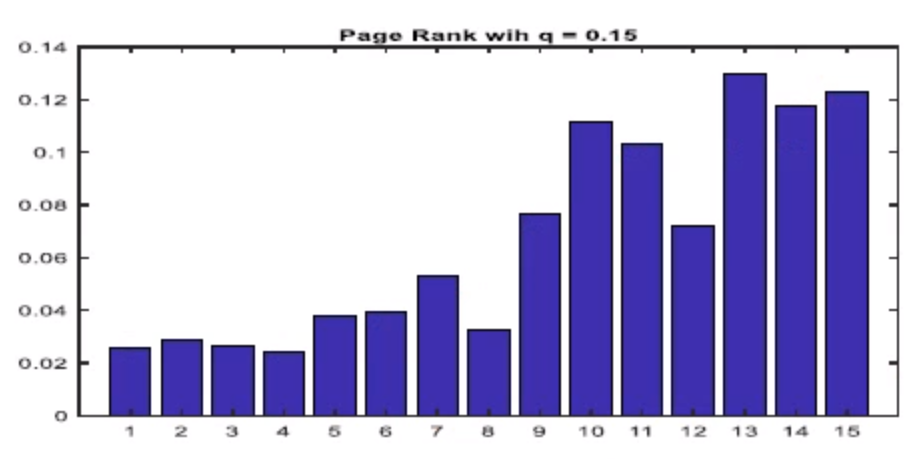

As you can see, the rank of Page 7 successfully exceed Page 6.

---

Let’s study the effect of removing Page 10 from the network (All links from Page 10 are deleted). Which page ranks increase, and which decrease?

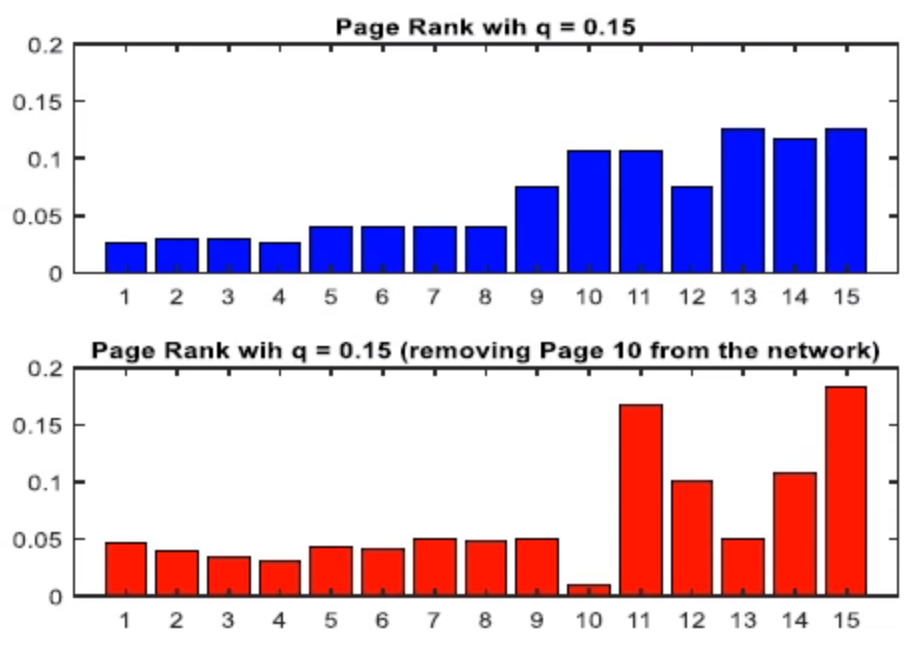
page	q = 0.15	q = 0.15 (Remove Page 10)	Increase or Decrease
1	0.0268	0.0462	Increase
2	0.0299	0.0393	Increase
3	0.0299	0.0341	Increase
4	0.0268	0.0305	Increase
5	0.0396	0.0426	Increase
6	0.0396	0.0412	Increase
7	0.0396	0.0496	Increase
8	0.0396	0.0481	Increase
9	0.0746	0.0506	Decrease
10	0.1063	0.0100	Decrease
11	0.1063	0.1669	Increase
12	0.0746	0.1005	Increase
13	0.1251	0.0492	Decrease
14	0.1163	0.1085	Decrease
15	0.1163	0.1826	Increase

There are 73% of the pages will increase, and 27% od pages will decrease. The reason is that, before removing Page 10, it can be seen that there are many pages (33% of the pages) point to Page 10, it means that Page 10 is relatively important to other websites.

Conclusion

PageRank is a powerful algorithm and has a wide application, such as ranking the football teams, ranking tweets in Twitter, or ranking track athletes. The merit of PageRank comes from its power in evaluating network measures in a connected system. Clearly, the surprisingly wide variety of these existing applications of PageRank point to a rich future for the algorithm in research contexts of all types. It seems intuitive that any problem in any field where a network comes into play might benefit from using PageRank.

References

1. [link] S. Brin and L. Page, The anatomy of a large-scale hypertextual web search engine
2. [link] Laurie Zack, Ron Lamb and Sarah Ball, An Application of Google’s PageRank to NFL Rankings
3. [link] Ashish Goel, Applications of PageRank to Recommendation Systems
4. [link] Clive B. Beggs, A Novel Application of PageRank and User Preference Algorithms for Assessing the Relative Performance of Track Athletes in Competition
5. [link] Shahram Payandeh and Eddie Chiu, Application of Modified PageRank Algorithm for Anomaly Detection in Movements of Older Adults