Laplace Expansion and Chiò Condensation

Determinants are mathematical objects which have applications in engineering mathematics. For example, they can be used in the solution of simultaneous equations, and to evaluate vector products. Determinants can also be used to see if a system of n linear equations in n variables has a unique solution. There are several ways to calculate determinant, however, today I’m going to introduce another way of computing determinants: Chiò Identity.

Introduction

In 1853 Felice (Félix) Chiò (1813–1871) published his short “Mémoire sur les fonctions connues sous le noms De Résultantes Ou De Déterminans”. In this article, I first give a way of evaluating determinants by Laplace Expansion, and explicitly comparing Chiò Identity to this.

Laplace Expansion Method

In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant of an matrix that is a weighted sum of the determinants of sub-matrices (or minors) of , each of size . The , cofactor of the matrix is the scalar defined by , where is the , minor of , that is, the determinant of the matrix that results from deleting the -th row and the -th column of .

class LaplaceDeterminants:
    def __init__(self):
        pass
    
    def minor_matrix(self, A, i, j):
        # Delete i-th row
        sub_A = np.delete(A, i, 0)
        # Delete j-th column
        sub_A = np.delete(sub_A, j, 1)
        return sub_A
    
    def calculate(self, A):
        n, m = A.shape
        if not n == m: 
            raise Exception("Must be a square matrix!")
        if n == 2:
            return A[0][0]*A[1][1] - A[1][0]*A[0][1]
        det = 0
        for i in range(n):
            M = self.minor_matrix(A, 0, i)
            det += (-1)**i * A[0][i] * self.calculate(M)
        return det

Chiò Condensation Method

The statement of Chiò Condensation is: let be an matrix, and let . Replace each element in the sub-matrix, let’s called it , of obtained by deleting the th row and th column of by:

Then .

class ChioDeterminants:
    def __init__(self):
        pass
    
    def calculate(self, A):
        n, m = A.shape
        if not n == m: 
            raise Exception("Must be a square matrix!")
        if n == 2:
            return A[0][0]*A[1][1] - A[1][0]*A[0][1]
        if A[-1][-1] == 0:
            for i in range(n):
                if A[0][i] != 0:
                    A[:, [i, n-1]] = A[:, [n-1, i]]
                    A[[0, n-1], :] = A[[n-1, 0], :]
                    break
                else:
                    return 0
        D = np.zeros(shape=(n-1, n-1))
        for i in range(n-1):
            for j in range(n-1):
                D[i][j] = A[i][j]*A[-1, -1] - A[-1][j]*A[i][-1]
        det = (1/A[-1][-1]**(n-2)) * self.calculate(D)
        return det

Performance

def test_laplace(n_samples=50000):
    algo = LaplaceDeterminants()
    for i in range(n_samples):
        A = np.random.rand(5, 5)
        det = algo.calculate(A)

def test_chio(n_samples=50000):
    algo = ChioDeterminants()
    for i in range(n_samples):
        A = np.random.rand(5, 5)
        det = algo.calculate(A)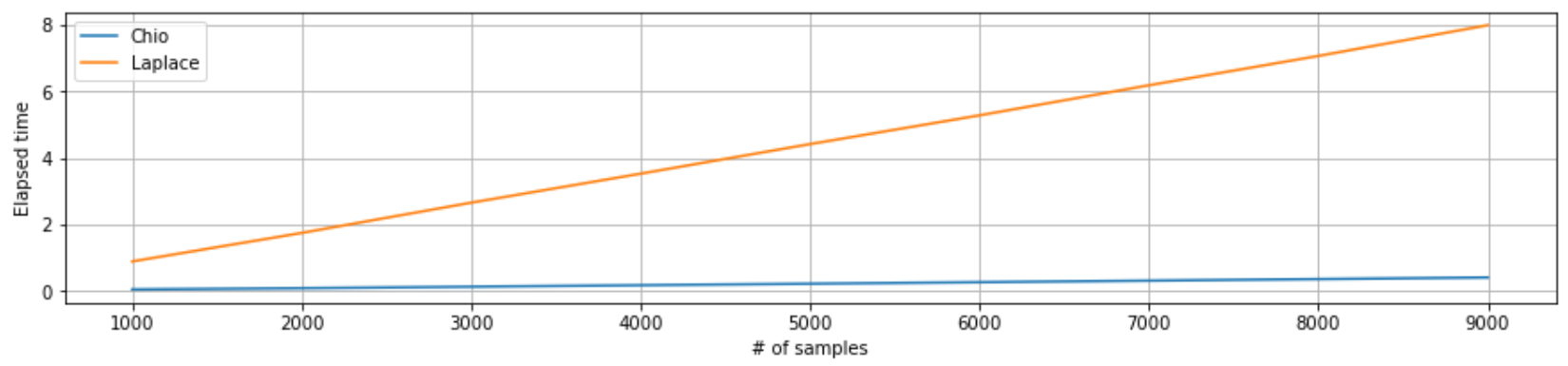

What if we also compare Chiò Condensation Method to numpy and scipy? They both computed determinants via LU factorization, relying on BLAS and LAPACK to provide efficient low level implementations of standard linear algebra algorithms.

def test_numpy(n_samples=50000):
    for i in range(n_samples):
        A = np.random.rand(5, 5)
        det = np.linalg.det(A)

def test_scipy(n_samples=50000):
    for i in range(n_samples):
        A = np.random.rand(5, 5)
        det = linalg.det(A)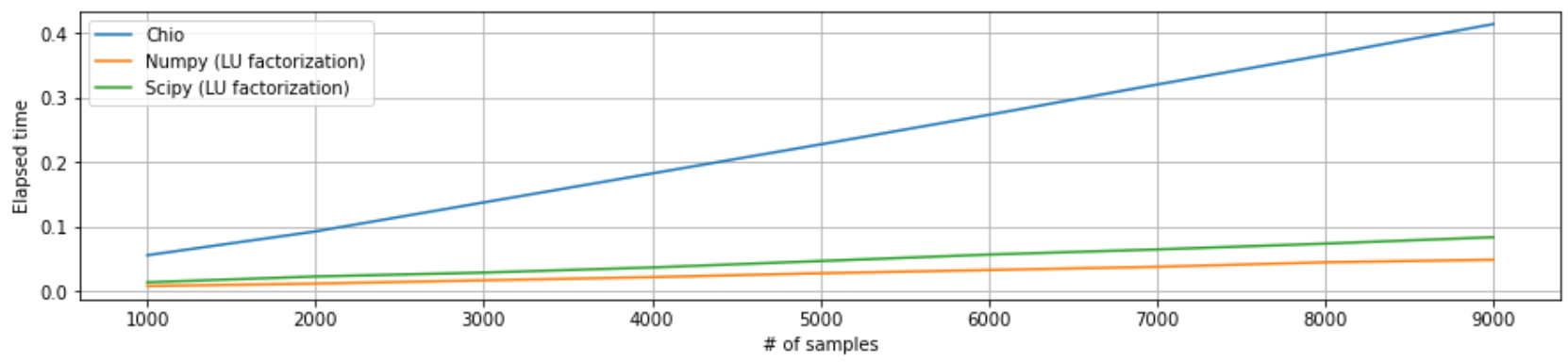

Quantstart has implemented an LU Decomposition directly over here, which does not rely on any external libraries.

Conclusion

Clearly, Chiò Condensation Method is much quicker than Laplace Expansion Method by minors, which yeilds complexity computation of . As an alternative method for hand-calculating determinants, therefore, Chiò’s method is quite effective. For numerical computations of large determinants on a computer, however, Chiò’s method is not so efficient as other methods such as, for example, Gaussian elimination, because of certain difficulties with round-off errors. In addition, Chiò’s method requires approximately multiplications, whereas Gaussian elimination requires approximately .

References

1. https://www.sciencedirect.com/science/article/pii/S0024379514002249
2. https://www.codeformech.com/determinant-linear-algebra-using-python/
3. https://en.wikipedia.org/wiki/Laplace_expansion
4. https://stackoverflow.com/questions/16636858/complexity-computation-of-a-determinant-recursive-algorithm
5. https://www.youtube.com/watch?v=UlWcofkUDDU.
6. Fuller, L. E., & Logan, J. D. On the Evaluation of Determinants by Chiò Method, 1975